Effectively designing and using portable, battery-based electrical circuits opens the door to creating autonomous hybrid systems. Understanding how to design a battery-powered, or direct current (DC), electrical circuit requires determining the following things:
Operators should establish a power budget in order to select technologies that are appropriate for their given applications and available resources. Establishing a budget is the first step in ensuring the solution is effective and provides as much autonomy as possible for the operator.
When establishing a budget, the operator must know the power requirements of the application before the portable power system can be configured properly. Establishing a budget sufficient for the task is important, because the ironclad rule of power generation is power generated in the circuit must be greater than or equal to the power that will be consumed in the circuit.
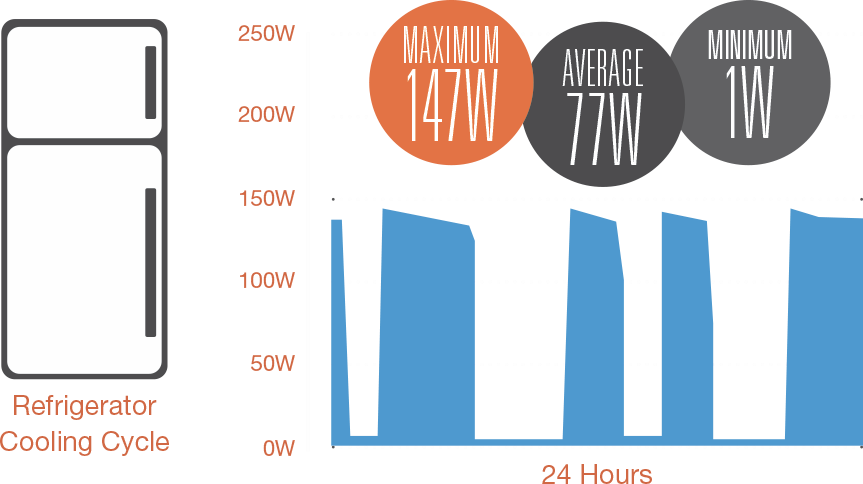
In any electrical circuit, electricity flows dynamically. Electricity flowing through the circuit varies in accordance with both the appliance requirements (loads that use power) and the power generators (devices that produce power).
For example, communication devices, medical equipment, lighting, and refrigerators all consume energy in a dynamic fashion: refrigerators only consume power when the thermostat calls for colder temperatures; communication radios consume more power when transmitting than when simply listening. Generator power production can fluctuate widely based on factors such as temperature, altitude, and fuel.
The portable, fuel-driven generator is still the primary mechanism or tool used in portable power applications. Users often choose fuel-driven generators for convenience. Powering appliances with a fuel generator is simple: just turn it on, plug in appliances, and refuel as needed.
Many AC appliances have Energy Star ratings to demonstrate that they operate more efficiently, using less power.
When determining the peak load of an appliance, experience has taught us that a general rule of thumb is to take the rated power consumption and multiply it by three to get a good estimate of the appliance peak or surge power:
Peak or Surge Power = 3 ∙ watts
Therefore, if an appliance is rated for 300 W continuous usage, then it is reasonable that the start-up load may be 900 W.
There are a few, noteworthy types of appliances that require very high peak start-up power:
Despite the highly refined mathematical methods and instrumentation we have today, it is still very difficult to calculate exact values for the power that is generated and consumed in a portable electrical circuit. Conversely, it is fairly simple to determine exactly how much power was generated and consumed in a circuit at the end of a period of time.
For example, many power generators today are rated, by their respective manufacturers, according to the maximum possible power output:
These ratings are often generated in a laboratory environment and do not take into account the derating (power degradation) often caused by operating environments (climate, altitude, location), type of fuel used, or a combination of factors. Similar effects lead to derating at the load, often for similar reasons. It is highly recommended the operator look at the total amount of power that flows through a closed electrical circuit over time as a game of averages.
The average load is the total energy delivered over a particular interval of time.
| A | = W ÷ V |
| amps | = watts ÷ 12 |
| W | = V ∙ A |
| watts | = amps ∙ 12 |
STIKmann owns a recreational vehicle (RV) and wants to build a DC electrical system to power it. His camper has two appliances (the load) in the electrical system, a 12 VDC refrigerator and a 12 VDC lamp, with each appliance consuming different amounts of energy.
Most electrical appliances have a specification plate or tag that tells what type and how much power is necessary to operate the appliance. If no specification plate is present, consult the manufacturer’s product literature. Depending on the manufacturer, you may find the operating energy requirement rated in watts or amps. If you know the voltage, you can use either value (watts or amps) to determine the other.
STIKmann’s 12 VDC lamp consumes 25 W of power, and he needs to know how much current (amps) it draws. He applies the formula as follows:
| W ÷ V | = A |
| 25 ÷ 12 | = A |
| = 2.1 A |
Now consider STIKmann’s refrigerator. The power consumption rating given on the refrigerator’s specification plate is 60 W. He uses the system voltage in the formula to determine the refrigerator draws 5 A of current when operating:
| W ÷ V | = A |
| 60 ÷ 12 | = A |
| = 5 A |
Both watts and amps can be tallied as a sum by adding the values together. To determine the total load values for the RV’s DC system—or the system’s total load—he adds the values of the wattage or the amperage for all of the individual appliances. The total amp draw for Stkimann’s lamp and the refrigerator is 7.1 A.
| 2.1 A + 5 A | = A |
| = 7.1 A total |
The total watt consumption for STIKmann’s lamp and refrigerator is 85 W.
| 25 W + 60 W | = W |
| = 85 W total |
Lastly, he calculates the total values for the system. The same formula applies and should reflect the overall characteristics of the circuit.
| V ∙ A | = W |
| 12 ∙ 7.1 | = 85.2 W |
It is common practice to round the numerical values for watts to the nearest whole number. In this case,
| 12 ∙ 7.1 | ≈ 85 W |
For STIKmann’s DC system, we determined the lamp and refrigerator draw a total current load of 7.1 A when both appliances are operating. However, this did not take into account that the lamp may not be in use all the time, or the refrigerator could be in operation for only 20 minutes every hour.
To get an accurate picture of his system’s total daily requirements, STIKmann must get the total hours per day of refrigeration and lamp operation time. Let’s say that he adds it all up and estimates that the total amp draw from the batteries is 7.1 A for 8 hours in a 24-hour period:
| 7.1 A ∙ 8 h | = 56.8 Ah |
This means STIKmann’s lamp and refrigerator consume about 57 Ah per day. In the same manner, the watt hours can also be calculated. STIKmann determines the refrigerator and lamp consume a total of 85 W and operate for a total of 8 hours daily:
| 85 W ∙ 8 h | = 680 Wh |
Then the total watt hours consumed by STIKmann’s appliances in a 24-hour period is 680 Wh. Even when labeled differently, the appliance energy requirements are exactly the same. With the appliances operating on 12 V multiplied by 56.8 Ah, a total load of 681 Wh is consumed:
| 12 V ∙ 56.8 Ah | = 681 Wh |
| (= 0.68 kWh) |
The total daily energy requirement for the STIKmann’s light and refrigerator is about 0.68 kWh.
Now that he knows how much energy he needs for the light and refrigerator on a daily basis, his next steps are to determine the correct battery capacity and how to replace the 57 Ah or 0.68 kWh of power consumed from the battery during one day.
We consider ourselves authorities in portable power and students of its application. STIKopedia reflects that and is updated continuously as the industry grows and evolves.
Questions? Comments? Click the compass at the upper left to contact us.
Battery Voltage
Battery voltage, or state of charge (SOC), of a lead-acid battery can be estimated by measuring the open (no load) battery terminal voltage using a digital voltmeter. Prior to measuring, the battery must have rested for 4 to 8 hours after charge or discharge and resided at a steady room temperature. With these conditions met, voltage measurements provide an amazingly accurate SOC for lead-acid batteries.
Specific Gravity
Specific gravity can be measured in wet-cell batteries with removable caps that provide access to the electrolyte. To measure specific gravity, you must use a tool called a temperature-compensating hydrometer, which can normally be purchased at an auto parts store or tool supply.
Load Testing
Load testing removes and measures the amps from a battery, similar to what happens when you start the engine of a car. Some battery companies label their battery with the amp load for testing. This number is usually about half of the CCA rating. A battery rated at 500 CCA would therefore be load-tested at 250 amps for 15 seconds.
A load test can only be performed if the battery is at or near a full charge. Some electronic load testers apply a 100-amp load for 10 seconds, and then display battery voltage. This number is then compared to a chart on the tester, which compares common load testing results to CCA ratings to determine battery condition.
Solar Stik uses only lithium iron phosphate (LiFePO4) battery chemistry in its lithium-ion energy storage products because it has safety characteristics similar to lead-acid batteries. LiFePO4 uses a nonflammable electrolyte, so when it’s completely discharged it becomes inert, making it safe for users.
In some lithium-ion polymer batteries, improper charging and storing can cause the formation of crystalline “needles” that can puncture the internal separator, resulting in failure or fire. This is not the case with LiFePO4 batteries because the reactants that store the charge are not flammable. All other lithium battery chemistries are volatile, reactive, and flammable, and if they do overheat and catch fire, conventional halon fire extinguishers will not put out the fire.
Common LiFePO4 cell types include cylindrical and prismatic (LiFePO4 chemistry is not packaged in pouch cells, another lithium cell type). It is easy to see how these were named, as they are actual descriptions of their physical attributes; they look like what they sound like.
Cylindrical
LiFePO4 cylindrical cells are all made of the same basic components. Each cell, and the entire battery, is enclosed by a resilient plastic container. Inside the container there is a “rolled” foil, and between the foil there is a layer of permeable “separator” material. A safe, nonflammable electrolyte (unique to LiFePO4) is added to each cell and saturates the “foil” and “separator”. The battery terminals are typically threaded (rather than posts) so that heavier-duty connections can be made to the load.
LiFePO4 is slightly less powerful than other commercially available lithium chemistries, but for many applications, the safety of its chemistry makes it the best choice despite its lower energy density. A LiFePO4 battery can be installed safely in any orientation. Safety vent valves are usually not required because the battery management system (BMS) will not allow the battery to overheat and vent gasses.
History of Lithium-ion Batteries
Experimental lithium batteries were developed as early as 1912, but it took nearly 70 years before a commercial lithium battery was developed for a wide market. Today, lithium batteries are most associated with enhancing “portable” capabilities. For example, they are the standard battery technology for high performance in portable electronics ranging from cell phones to laptop computers. There is a diverse family of lithium chemistries available. At first glance, they might all seem to be the same, but there are exploitable, distinct differences between them. The unique nature of the various chemistries allows each type to fill special application niches.
Even with wide market adoption in the early 1990s, as societal demands for lightweight portable electronics was burgeoning, the high cost barrier and complexities in battery management circuits would prevent lithium batteries from being used widely in support of larger devices or in scaled energy-storage systems such as large vehicles or uninterruptible power supply (UPS) systems.
Today, lithium battery technology continues to evolve at a rapid pace. Manufacturers, driven by demands from new applications, are constantly pushing the envelope by making changes in the chemistry and structure in search of improved battery life and greater energy density.
Lead-acid batteries are the most commonly used batteries and come in several different configurations. The oldest of the lead-acid battery types are flooded-cell (or wet-cell) batteries and can be either the sealed or the open variety. In both types, the electrolyte evaporates due to charging, age, or ambient heat.
In the mid 1970s, a “maintenance-free” valve-regulated lead-acid (VRLA) battery was developed.
VRLA batteries can be absorbed glass mat (AGM) or gel cells. Solar Stik uses AGM batteries in its lead-acid products.
VRLA batteries remain under constant pressure of 1–4 psi. This pressure helps the recombination process during charging when more than 99% of the hydrogen and oxygen generated are turned back into water.
Unlike the flooded lead-acid battery, VRLA batteries are designed with a low overvoltage potential, which prohibits the battery from reaching its gas-generating potential during charge. This safeguard prevents excess charging, which would cause gassing and electrolyte depletion.
History of Lead-acid Batteries
Lead-acid is the oldest rechargeable battery technology in existence. Invented by the French physicist Gaston Planté in 1859, lead-acid was the first rechargeable battery to be used in commercial applications. More than one hundred fifty years later, we still have no real cost-effective alternatives for cars, boats, RVs, wheelchairs, scooters, golf carts, and UPS systems.
The lead-acid battery is still the most widely used 12 V energy storage device. A lead-acid battery is an electrical storage device that uses a chemical reaction to store and release energy. It uses a combination of lead plates and an electrolyte to convert electrical energy into potential chemical energy and back again.
There are many newer battery technologies available in the marketplace. However, lead-acid technologies are better understood and are widely accepted as the standard by which all other batteries are measured. Newer technologies often have operational constraints, including maximum and minimum operating temperatures and special charging requirements that make them less versatile and useful for the average consumer in everyday applications.
Flexible solar PV panels fuse form factor with capability and deliver maximum power generation with minimum weight. Flexible panels use amorphous silicon or copper indium gallium selenide (CIGS) thin-film technology, which can be used with many substrate options that allow flexible panels to be folded or rolled.
Solar Stik uses extremely rugged, paper-thin, flexible PV panels that can withstand harsh conditions.
As the name implies, thin-film solar PV cells lack the thickness of other PV technologies. Composed of a very thin layer of substance on a substrate, today’s thin-film cells are one percent as thick as the first manufactured silicon solar cells.
Foldable or rollable thin-film panels make storage and transport convenient. For low-power applications that require portability, thin-film solar PV panels are an excellent option.
Numerous thin-film solar PV technologies exist today. However, they are slightly less efficient than other types of PV cells, so more surface area is required to generate the same amount of power. Most thin-film panels are designed for single-device applications, like recharging a battery-operated device.
The two most common types of thin-film solar PV panels are amorphous silicon and copper indium gallium selenide (CIGS).
Amorphous Silicon Solar PV Panel
Amorphous silicon is the oldest thin-film technology and arguably the best. When laid on a substrate, amorphous silicon does not require a grid configuration to conduct electricity, allowing it to be used on large areas with ease. However, it does not conduct as well as crystalline silicon solar PV cells used in rigid panel technology because the connections between the silicon atoms are not as consistent. This inconsistency results in interrupted electron flow.
Numerous substrate materials can be used with amorphous silicon, making the technology highly adaptable. Polymer plastic is one option for substrate. Because polymer plastic is flexible and able to be folded or rolled, it excels in applications requiring ease of storage or transport.
Amorphous silicon solar PV panels perform better in low light intensities. This makes amorphous silicon a good choice for environments with interrupted sunlight or dusty conditions.
Rigid solar PV panels are ideal for stationary applications that require maximum power and a small installation footprint. They are the first generation of solar PV panels, provide more power per square foot than other PV panel types, and are highly durable. Rigid panels do not degrade significantly over time, making them a good choice for long-term investment.
Solar Stik uses both multi- and monocrystalline, glass and non-glass—impact-resistant and shatterproof—rigid panels.
Rigid solar PV panels are typically made of glass or non-glass panels and aluminum frames. Rigid panels are among the best performing panels, but their physical characteristics make them a poor choice for certain applications—especially when portable power is desired.
Travel and storage can be difficult because rigid panels often contain breakable glass and cannot be folded.
The Solar Stik system design overcomes many of the physical challenges associated with the rigid panels. This results in portable power systems that draw from the best available PV technology.
The two main types of rigid solar PV panels are monocrystalline and multi- or polycrystalline.
A rigid monocrystalline solar PV panel is distinctly recognizable by the arrangement of the individual solar PV cells (squares with no corners) that appears as a uniform, flat color.
The surface of a rigid multi- or polycrystalline solar PV panel has the appearance of a rectangular grid and more of a bluish speckled color.
Performance differences between rigid solar PV panels can be experienced in high operating temperatures and shaded conditions. Monocrystalline panels perform better in higher external temperatures and full sun. Multi- or polycrystalline panels suffer performance losses in higher heats but have slightly higher outputs compared to monocrystalline panels when the panel is partially shaded.
The role of the battery management system (BMS) is simple: It controls the actual voltage of each cell, so that it doesn’t get too high or too low.
2Prolong the life of the battery
3Maintain the battery in a state in which it can fulfill the functional requirements of the application
To achieve these objectives, the BMS may incorporate one or more of the following functions:
Cell Protection Protecting the battery from out of tolerance operating conditions is fundamental to all BMS applications. In practice the BMS must provide full cell protection to cover almost any eventuality. Operating a battery outside of its specified design limits will inevitably lead to failure of the battery. Apart from the inconvenience, the cost of replacing the battery can be prohibitive. This is particularly true for high voltage and high power automotive batteries which must operate in hostile environments and which at the same time are subject to abuse by the user.
Bricking a LiFePO4 Battery
As soon as the BMS senses that the cell voltage is too low to discharge, time is of the essence to place the batteries on charge. Failure to do this may cause a fatal error known as “bricking”. Once the batteries reach their internal disconnect voltage, the voltage can fall very rapidly in the internal cells, causing the battery to brick. This means that the battery cells are nonrecoverable, and the battery module must be replaced.
Specific gravity of the electrolyte can be defined as:
A measure of the density of the liquid electrolyte compared to the density of water at a specific temperature and pressure.
The chemical reaction takes place inside the pores of the active material on the battery’s lead plates. If the battery has just been charged, the electrolyte in the pores of these lead plates is very rich in sulfuric acid. As a result, the battery’s voltage will be high, perhaps as much as 13 to 14 volts. As the battery rests following a charge, its voltage slowly drops and then levels off as the electrolyte stabilizes its chemical state between the plates.
“Zero Gravity” by Scott Robinson is licensed under CC BY 2.0
A similar change in battery voltage occurs during discharge. During the battery discharge process, the electrolyte transfers its sulfur content to the lead plates. As the electrolyte loses sulfur, its specific gravity gets “lighter” or closer to that of water, indicating that the battery has been discharged. Because the specific gravity of the electrolyte is measurable, it can be used to determine the state of a battery’s charge and health. While a fully charged battery may read 12.68 volts, the voltage will drop and then stabilize at a somewhat lower value as a load is applied.
The change in voltage occurs even though the state of charge of the battery has not significantly changed. This is due to the local electrolyte in the pores of the plates becoming less rich in sulfur as the battery supplies current. As the battery discharges, electrolyte more like sulfuric acid enters the pores while electrolyte more like water exits the pores.
As discharge continues, the electrolyte in the pores eventually stabilizes at a specific gravity somewhat lower than the average value in the battery, producing the slightly lower battery voltage.
The operational characteristics of the lead-acid battery can be explained best by the terms capacity and cold-cranking amps (CCA).
Capacity is the amount of energy a battery can store. It is usually given in amp hours (Ah), or the amount of current measured in amps that the battery can provide over a period of one hour before rendering the battery discharged.
The secret of any battery’s runtime lies in the battery’s plate capacity. During charging and discharging, the lead on the plates gets gradually eaten away and the sediment falls to the bottom. The service life of a lead-acid battery can be measured by the thickness of the positive plates. The thicker the plates, the longer the life will be and the more energy storage you can expect.
The weight of a battery is another good indicator of the lead content and the life expectancy. Generally speaking, the heavier the battery, the more lead it contains and the longer it will last.
Most industrial flooded deep-cycle batteries use lead-antimony plates. Antimony is a metal that stiffens the lead plate and helps prevent battery failure due to structural failure of a plate. This improves the plate’s life but increases gassing and water loss. Antimony is not necessary in AGM batteries due to the rigid construction of the overall battery.
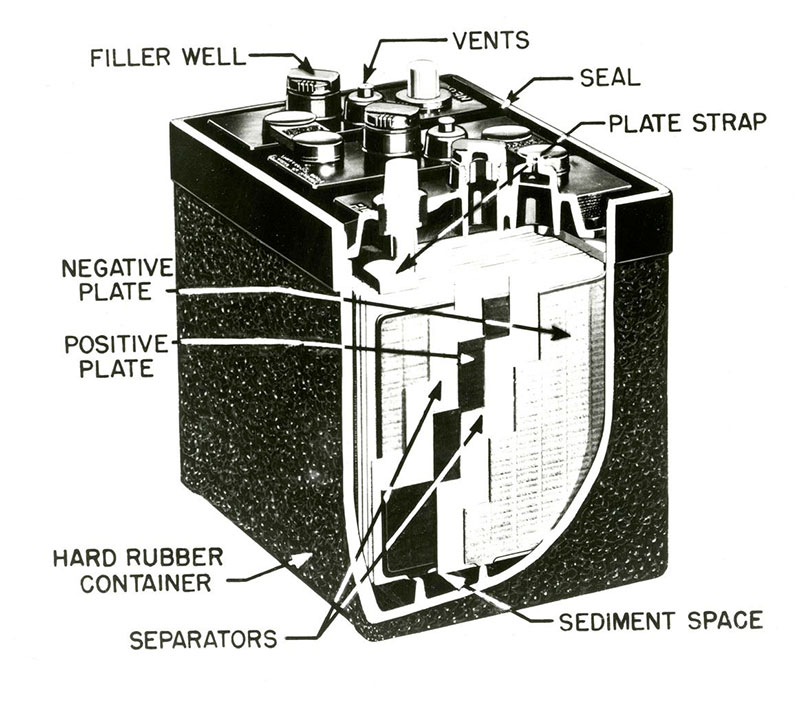
1953 automotive lead-acid battery
Cold-cranking amps (CCA) is the amount of energy a battery can deliver in short bursts. It is the maximum amount of current (amps) that a battery can deliver at 0 °F for 30 seconds without dropping below 7.2 volts. A high CCA battery rating is good, especially in cold weather. Starter batteries are often rated in CCA and are designed to deliver a short-duration burst of power, such as that required to start a vehicle.
Age and environmental conditions can affect the capacity and the CCA. As a battery ages, capacity and CCA will not degrade at the same rate. CCA tends to stay high through most of the battery’s life, but it drops quickly towards the end. If you drive a car, you’ve probably experienced this when, near the end of the battery’s life, suddenly the battery won’t start the car in the morning.
Capacity decreases gradually. A new battery is designed to deliver 100% of its rated capacity. As the battery ages, the capacity steadily drops and it should be replaced when its ability to store power falls below 70% of its original rating.
The overall health of a battery is most directly related to its capacity, not its CCA. As noted before, the CCA remains within the optimal range for most of a battery’s life, so performance and health declines will be most notable in the loss of capacity.
The illustration shows two fully charged lead-acid batteries, one with a high capacity and one that has aged. The buildup of visible “rock content” (crystalline formation, also called sulfation or memory) due to aging robs the battery of usable capacity, although the battery may still provide good cranking power.
Appliance efficiency is also known as load efficiency. As appliances consume less power, power source requirements also change. When designing a portable power system, purchasing highly efficient components can provide many benefits.
Appliance loads can often be matched to the electrical characteristics of the circuit. This will increase the system’s overall efficiency by allowing direct connection to the circuit without the need for additional power management devices to aid in the function.
The fewer management components used in a system, the more efficiently it will operate. For example, components such as inverters, converters, or similar devices used in a circuit to “adapt” appliances for use in a particular electrical circuit themselves require power to operate, and thus the total power required to operate the appliance is increased.
For example, a 12-volt direct current (DC) electrical circuit powered by a 12 V battery can directly support a refrigerator that also operates at 12 VDC. This setup will transfer power through the circuit more efficiently than if the refrigerator requires 120 V alternating current (AC) power. In the latter example, an inverter would be required.
It is prudent to shop around when looking for appliances because power consumption varies among models even within a particular appliance class. Purchasing an energy-efficient device can be more expensive up front, but could mean future savings in energy costs as well as a flexibility of use that makes the device compatible with a variety of portable power sources. When purchasing an electrical appliance, remember to ask if a 12 VDC adapter is available for the product.
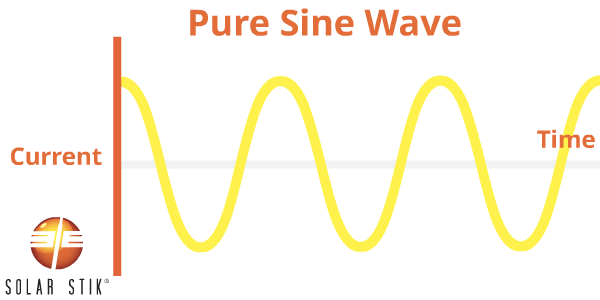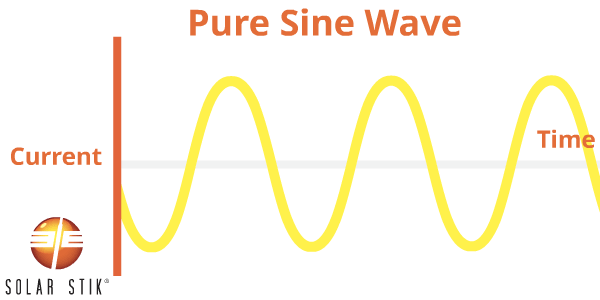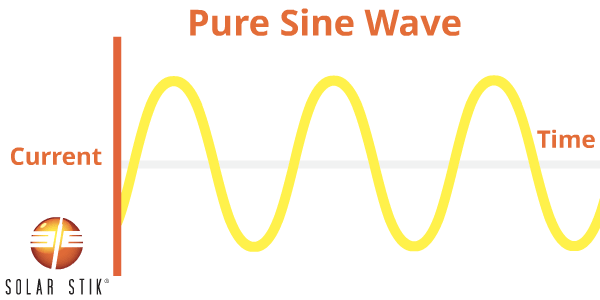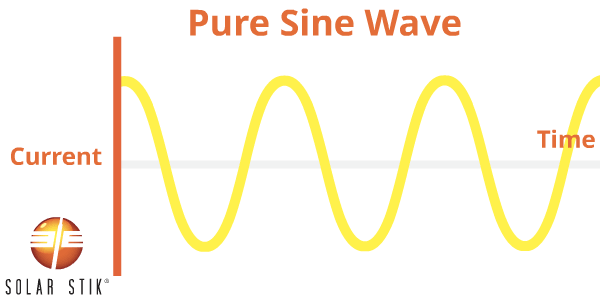
A pure sine (also referred to as a sinusoidal) wave can be produced by rotating machinery (a generator). This is the type of waveform provided by electric utility companies. This type of power is available anywhere an outlet is tied to the power grid, such as in homes or businesses.
A PSW inverter reproduces this waveform through the use of advanced internal circuitry.
A modified sine wave (also referred to as non-sinusoidal or step-wave) inverter is different from a pure sine wave power inverter because the modified waveform output is step-shaped.
AC appliances that are not specifically designed to work with this type of inverter waveform output may take more power to operate, thereby reducing the efficiency of the entire electrical system. For example, some appliance motors may produce more heat and burn out when they are operating.
Other appliances that use electronic controls will not be able to vary speed or temperature when using modified sine wave power. Some fluorescent lighting may not get as bright or may make buzzing noises. Appliances with digital clocks or electronic timers may not work properly with this type of inverter because the waves are rougher and cause extra noise to be created in the circuitry.
The following appliances may experience problems when operated from MSW inverters:
Low-wattage Inverters
Most vehicle starting batteries will support a low-wattage inverter for short time periods. Actual operating time will vary depending on the age and condition of the battery, the Ah capacity of the battery, and the AC appliance powered by the inverter. If you use a low-wattage inverter that is powered through a DC accessory socket, and the vehicle engine is turned off, you should periodically run the engine to recharge the battery.
Medium- and High-wattage Inverters
It is strongly recommended that only deep-cycle batteries be used for any inverter with a continuous output of 200 W or more. This will ensure that you have several hundred complete charge and discharge cycles. If you use a normal vehicle starting battery to support a medium- or high-wattage inverter, it will quickly fail after repeated charge/discharge cycles (since starting batteries are not designed to perform this type of work).
When the inverter operates power-hungry appliances with continuous loads for extended periods, it will drain the battery to the point where the battery has insufficient energy to support the inverter. In these cases, it’s a good idea to have additional deep-cycle batteries available to extend the appliance operating time.
Lead-acid batteries are the most commonly used batteries and come in several different configurations. The oldest of the lead-acid battery types are flooded-cell (or wet-cell) batteries and can be either the sealed or the open variety. In both types, the electrolyte evaporates due to charging, age, or ambient heat.
In the mid 1970s, a “maintenance-free” valve-regulated lead-acid (VRLA) battery was developed.
VRLA batteries can be absorbed glass mat (AGM) or gel cells. Solar Stik uses AGM batteries in its lead-acid products.
VRLA batteries remain under constant pressure of 1–4 psi. This pressure helps the recombination process during charging when more than 99% of the hydrogen and oxygen generated are turned back into water.
Unlike the flooded lead-acid battery, VRLA batteries are designed with a low overvoltage potential, which prohibits the battery from reaching its gas-generating potential during charge. This safeguard prevents excess charging, which would cause gassing and electrolyte depletion.
History of Lead-acid Batteries
Lead-acid is the oldest rechargeable battery technology in existence. Invented by the French physicist Gaston Planté in 1859, lead-acid was the first rechargeable battery to be used in commercial applications. More than one hundred fifty years later, we still have no real cost-effective alternatives for cars, boats, RVs, wheelchairs, scooters, golf carts, and UPS systems.
The lead-acid battery is still the most widely used 12 V energy storage device. A lead-acid battery is an electrical storage device that uses a chemical reaction to store and release energy. It uses a combination of lead plates and an electrolyte to convert electrical energy into potential chemical energy and back again.
There are many newer battery technologies available in the marketplace. However, lead-acid technologies are better understood and are widely accepted as the standard by which all other batteries are measured. Newer technologies often have operational constraints, including maximum and minimum operating temperatures and special charging requirements that make them less versatile and useful for the average consumer in everyday applications.
Lead-acid batteries are commonly made of five basic components:
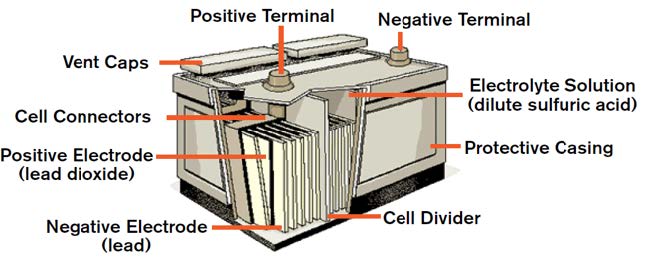
A battery cell is a container in which electrolyte and lead plates can interact. The electrolyte is usually a solution made up of 35% sulfuric acid and 65% water. The lead plates are treated with lead oxide and powdered sulfates to give them their positive and negative properties.
When the positive and negative lead plates are submerged in the battery’s electrolyte, a chemical reaction occurs. This reaction causes electrons to flow between the lead plates. The negative lead plate builds up an excess of electrons in a process called oxidation. This causes an electrical difference between the negative plate and positive plate.
The extra electrons on the negative lead plate want to displace the electrons on the positive plate in a process called reduction. However, the electrolyte solution of sulfuric acid and water ensures the electrons cannot travel directly to the positive plate. When the circuit is closed (with the help of a “conductive path”, or load, between the negative and positive plates), the electrons are able to travel to the positive plate. This, in turn, provides power to any appliance placed along the path.
This electrochemical process can be summarized as a reversible transfer of sulfate between the water and the lead plates during charging and discharging. As the battery is discharged, sulfate in the solution combines chemically with the lead plates of the battery to form lead sulfate. As the plates accumulate this sulfate, the electrolyte solution becomes more like water and less like sulfuric acid. The reverse occurs as the battery is charged. As charging current flows into the battery, the battery plates revert back to their original condition and the electrolyte reverts back to its original sulfuric acid content.
Lithium-ion batteries are made of the following basic components:
The exact chemistry is often patented and proprietary to each battery maker.
When a charge is applied to a lithium-ion battery, electrons flow between the internal components. The basis of this reaction is the lithium metal binding and unbinding with the other chemicals in the electrodes at the ionic level. As power is drawn out of the battery, the metal moves from one electrode to the other, and when the battery is charged, it moves back to the original state. The metallic lithium ions literally move through the separator material.
The Primer
Power Generation
Energy Storage
System Architecture
Electricity Basics
Power Management
Circuits
